한빛출판네트워크

알고리즘은 어떤 일을 하기 위한 명령의 집합입니다. 이런 의미에서 모든 코드를 알고리즘이라고 부를 수 있겠지만,  대개는 다른 코드보다 속도를 빠르게 하거나, 아주 흥미로운 문제를 풀기 위한 것을 뜻합니다. 몇 가지 예를 들어 볼게요.
 

• 이진 탐색 알고리즘을 사용하면 코드의 속도를 빠르게 할 수 있습니다. 예를 들어 실행해야 할 단계가 40억 단계에서 32단계로 줄어들 수 있습니다.
• 내비게이션은 그래프 알고리즘을 사용해서 목적지까지의 최단 경로를 계산합니다.
• 동적 프로그래밍을 사용하면 체커 게임을 하는 인공지능 알고리즘도 구현할 수 있습니다.

모든 알고리즘은  프로그래밍 언어가 무엇이든 간에 대부분 이미 구현되어 있을 것입니다. 그러므로 우리가 모든 알고리즘을 직접 코딩해야 할 필요는 없습니다. 하지만 알고리즘 간 차이점을 이해하지 못한다면 미리 구현해 놓은 알고리즘은 별로 쓸모가 없습니다. 병합 정렬을 사용해야 할까요? 아니면 퀵 정렬을 사용해야 할까요? 혹은 배열과 리스트 중 어느 것이 더 좋을까요? 단순히 다른 자료구조를 사용하는 것만으로도 성능이 크게 달라질 수 있습니다.

방금 예시로 들었던 알고리즘 중 이진 탐색(Binary Search)에 대해 알아보겠습니다. 코딩 테스트에서 자주 출제되고 실무에서도 많이 활용되는 기본적인 알고리즘입니다.

✅이진 탐색(Binary Search)

전화번호부에서 누군가의 번호를 찾고 있는 중이라고 가정해 볼게요(옛날에는 전화번호부란 책자가 있었어요!). 찾을 사람은 박씨입니다. 어떻게 찾는 것이 좋을까요? 전화번호부의 처음 ㄱ부터 ㅂ으로 시작되는 이름이 나올 때까지 페이지를 한 장씩 차례대로 넘기면서 찾는 방법이 있습니다. 하지만 그 방법보다는 일단 책 한가운데를 펼치는 방법을 사용하는 게 더 좋겠죠? 가나다 순서대로라면 전화번호부의 중간쯤에 박으로 시작되는 이름이 있을 테니까요.

사전에서 단어를 찾을 때도 마찬가지죠. 찾으려는 단어가 알파벳 O로 시작한다면 마찬가지로 사전의 중간부터 펼쳐 볼 겁니다. 

페이스북에 로그인한다고 생각해 보세요. 페이스북은 일단 우리의 계정이 진짜로 존재하는지 확인하기 위해 데이터베이스에서 아이디를 찾아야 합니다. 아이디가 “karlmageddon”이라고 가정해 볼게요. 페이스북은 알파벳 A부터 시작해서 차례대로 이 아이디를 찾을 수도 있겠지만, 중간 어디쯤에서 찾기 시작하는 것이 더 나을 수도 있습니다.

이런 문제를 탐색^search 문제라고 합니다. 그리고 앞에서 예로 든 모든 경우에 이진 탐색^{binary search}이라는 알고리즘을 사용할 수 있습니다. 이진 탐색은 알고리즘입니다. 입력으로는 정렬된 원소 리스트를 받습니다. 이진 탐색 알고리즘은 리스트에 원하는 원소가 있으면 그 원소의 위치를 반환하고, 아니면 null 값을 반환합니다.

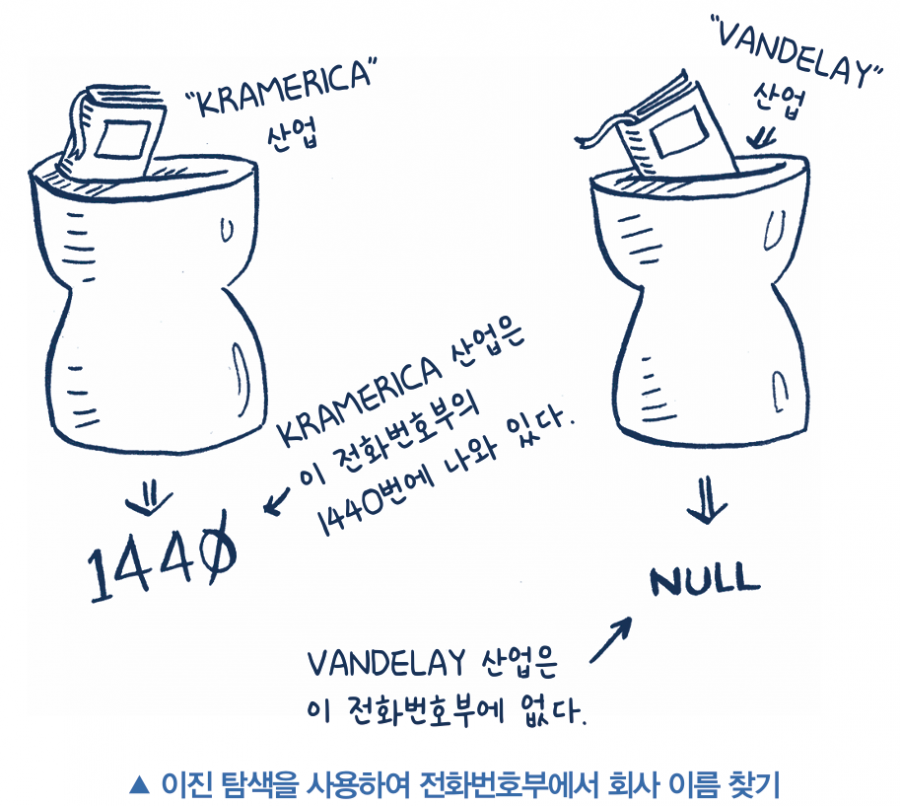
이진 탐색이 어떻게 작동하는지 예를 들어 볼게요. 1과 100 사이 숫자를 하나 생각합니다.  이제 가능한 한 가장 적은 횟수의 추측으로 이 숫자를 알아내야 합니다. 한 번 추측할 때마다 찾아야 하는 숫자보다 제시한 숫자가 더 작은지, 더 큰지, 맞는 숫자인지 알 수 있습니다. 만약 1, 2, 3, 4, … 순서대로 모두 추측한다고 하면 다음 그림과 같겠죠.

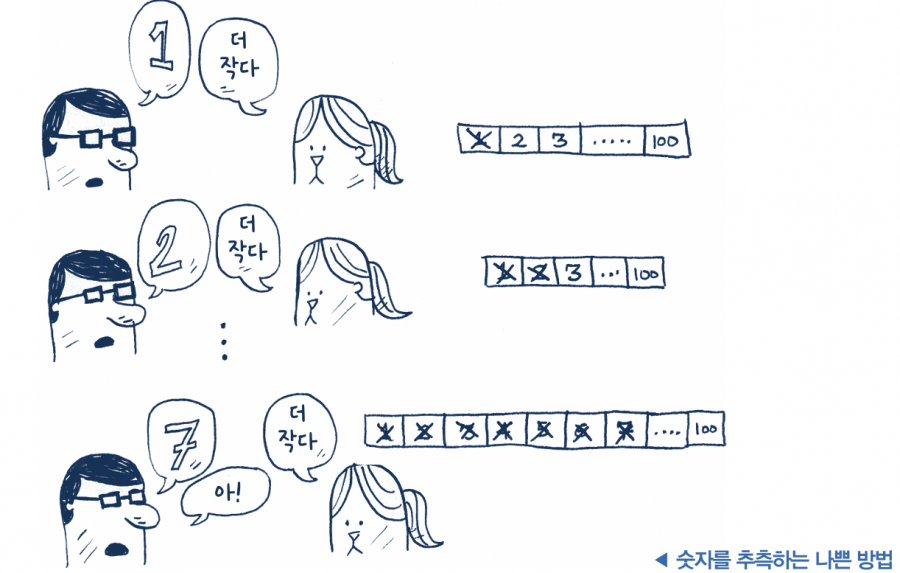
이런 방법을 단순 탐색^{simple search}(바보 같은 탐색이라는 말이 더 맞을지도 몰라요)이라고 합니다. 한 번 추측할 때마다 추측한 숫자 하나가 답이 아니라는 것을 알게 될 뿐입니다. 만약 답이 99라면 답에 도달하기까지 99번 추측해야 합니다.

• 더 좋은 탐색 방법

더 좋은 방법이 있습니다. 100의 중간, 즉 50부터 시작하는 방법입니다.

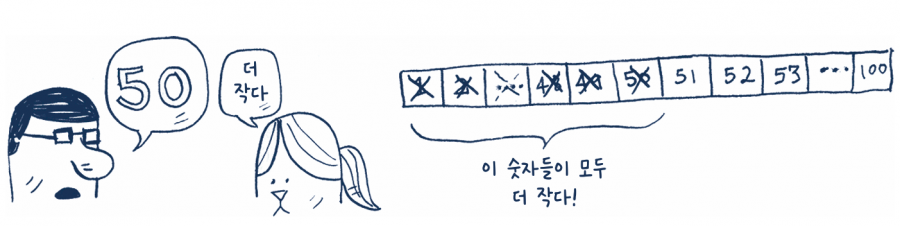
“50이 더 작다”라는 대답 하나로 숫자의 절반이 답이 아니라는 것을 알 수 있습니다! 1부터 50까지의 숫자가 더 작다고 하니까 이번에는 남은 51과 100까지의 숫자 중 중간에 해당하는 75로 추측해 봅니다.

75가 더 크다는 것을 알았으므로 앞에서와 마찬가지로 75와 같거나 더 큰 숫자들을 제외할 수 있습니다. 이진 탐색에서는 매번 남은 숫자 중 가운데 숫자를 말하고 대답에 따라 그보다 큰 혹은 작은 숫자들을 한꺼번에 없앨 수 있습니다. 다음으로는 63(50과 75의 중간)이 정답인지 추측해 봅니다.

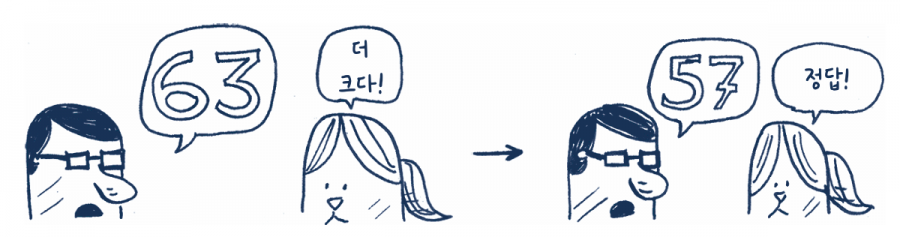
이것이 바로 이진 탐색입니다. 우리는 방금 알고리즘을 하나를 배웠습니다! 얼마나 많은 숫자를 답에서 제외했는지 다시 살펴볼게요.

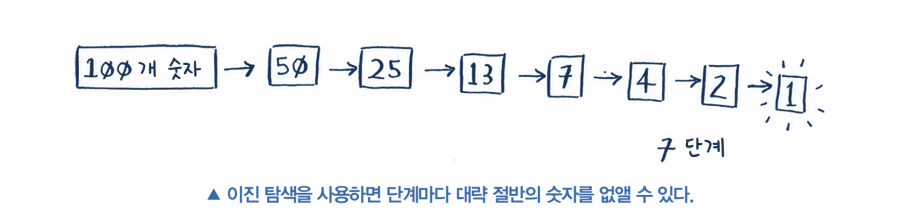
한 번에 아주 많은 숫자를 제거할 수 있기 때문에 어떤 숫자가 답이 되든지 최대 7번 만에 정답을 맞힐 수 있습니다. 이번에는 사전에서 단어를 찾고 있다고 가정해 볼게요. 이 사전에는 단어가 240,000개 있습니다. 최대 몇 번 만에 정답을 찾을 수 있을까요?

만약 찾으려는 단어가 사전의 제일 끝에 실려 있다면 단순 탐색으로는 240,000번 추측해야 하겠죠. 하지만 이진 탐색으로는 남은 단어의 절반을 한 번에 제외시킬 수 있습니다.

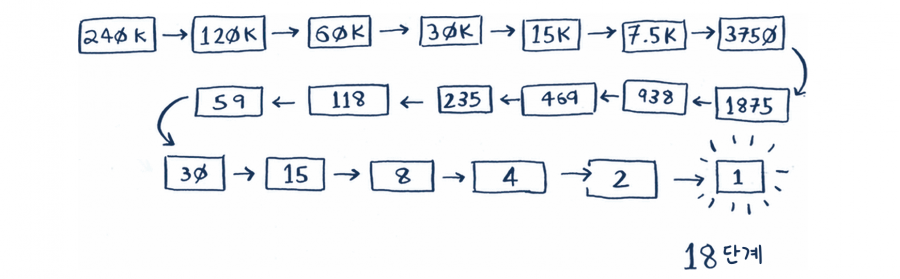
그러니까 이진 탐색으로는 18번 만에 정답을 찾을 수 있습니다. 단순 탐색과 비교가 안 되죠! 만약 n개 원소를 가진 리스트에서 이진 탐색을 사용하면 최대 log₂n번 만에 답을 찾을 수 있습니다. 단순 탐색이면 최대 n번이 필요할 수도 있습니다.

• 실행 시간

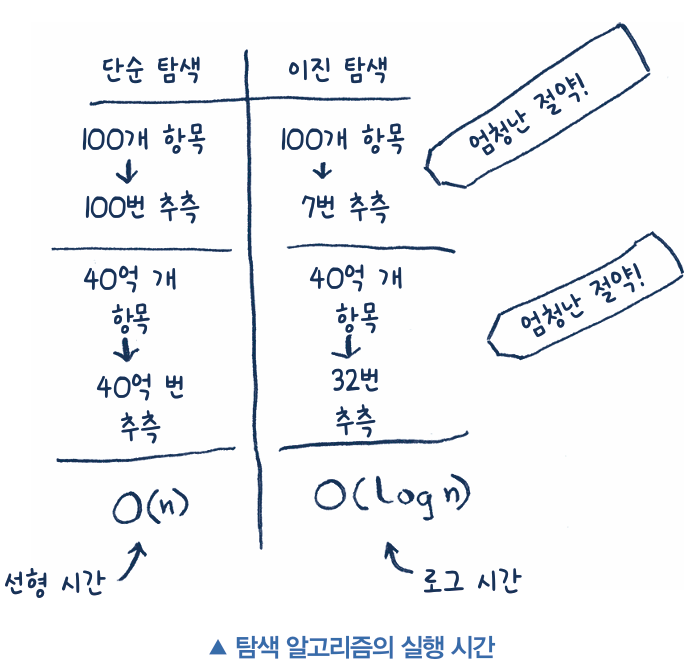
만약 이진 탐색을 사용하면 얼마나 많은 시간을 절약할 수 있을까요? 숫자를 하나하나 확인하는 단순 탐색을  쓰면 리스트에 100개 원소가 있는 경우 100번 추측해야 합니다. 만약 원소가 40억 개가 있다면 40억 번 추측해야 하죠. 그러니까 추측해야 할 최대 횟수는 리스트의 길이와 같습니다. 이를 선형 시간^{linear time}이라고 합니다.

이진 탐색은 다릅니다. 만약 리스트 안에 원소가 100개 있다면 7번만 추측해도 되죠. 리스트의 길이가 40억 개라고 해도 32번만 추측하면 됩니다. 굉장하지 않나요? 이진 탐색의 경우에는 로그 시간^{logarithmic time}으로 실행됩니다.

이진 탐색을 비롯하여 알고리즘을 공부하면, 지금까지 엄두 내지 못했던 문제를 해결하는 방법을 배울 수 있습니다. 예를 들면 이런 것들이죠.

• 비디오 게임을 만들고 싶다면 그래프 알고리즘을 이용해서 사용자를 따라다니는 인공지능 시스템을 만들 수 있습니다.
• KNN 알고리즘을 사용해 추천 시스템을 만드는 것을 배웁니다.
• 어떤 문제는 적절한 시간 내에 풀 수 없습니다! NP-완전 문제에 대한 내용에서는 어떤 문제가 적절한 시간 내에 풀 수 없는 문제인지 알아내고, 대략적인 답을 구할 수 있는 알고리즘을 보여 줍니다.

 새롭게 배운 지식을 기반으로 인공지능, 데이터베이스 등에서 사용되는 더 구체적인 알고리즘을 배울 수도 있고, 지금 하고 있는 일에서 어려운 부분을 해결할 수도 있습니다.

위 컨텐츠는 『그로킹 알고리즘(개정판)』의 내용을 재구성하여 작성되었습니다.